This is probably the first time I've ever solved all problems in Programming Competition. So, as to commemorate the event, I'm writing my solution about the problems.
Problem 1:
you can view it
here.
question: given
N percentage of a circle with radius 50 and center at (50, 50), determine whether point at
(X, Y) is within that circle or not.
Answer:
This problem is quite obvious, in this problem we just need to figure out the degree and distance of
(X, Y) from (50, 50).
The distance can be measured using basic trigonometry
r = sqrt(dx^2 + dy^2)
The degree can be measured with
arccos(dx / r)
Though we'll need a little tweak based on which quarter it's placed on.
tag:
Mathematic, Trigonometry, Implementation
Problem 2:
can be viewed
here.
problem is too long to be explained, checkout that link.
Answer:
This is a problem where, if you feel confused, just try to implement it.
The solution here is just to order the items in the descending order (or ascending if you're using stack).
1. Pick the most heavy item (last in the ascending ordered stack), we will call it
X
2. Based on that item, also pick
n - 1 item starting from the lightest where
n = Math.ceil(50 / B)
3. keep doing it, until all (
X *
n) < 50.
for example if our items:
[50, 30, 30, 10, 6, 5, 4, 3, 2, 1, 1, 1]
our pick will be:
- 50
- 30 and 1
- 30 and 1
- 10 and 1, 2, 3, 4
- 5 and 6 is left, we can ignore them and just assume that he has delivered it in the previous delivery.
tag:
Greedy
Problem 3:
details can be viewed
here
tl;dr: given N dice with M side, figure out the probability that the sums of all dice is greater than X.
Answer:
Ok, this one, is harder (Actually, I literally figured out the answer right after I wake up the next day lol).
The thought process:
Ok, I start with: ... I know this is probably binomial distribution, normal distribution, pascal triangle or something... but I couldn't figure out how I can use it to solve this problem?
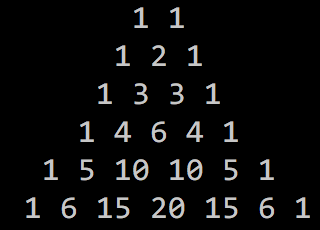 |
| Pascal Triangle for 2 sided coin. |
After a few times of thinking..., well doesn't hurt to get some insight, let's write some simulation... probably something like this?
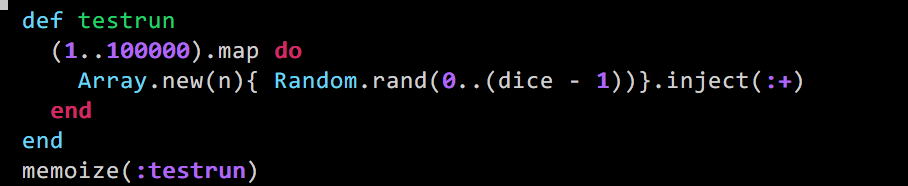 |
| Random Dice Generator. |
For non-rubyist, that code basically create 100.000 simulation throwing <dice>-sided dice <n>-times. and get the sum of those dices.
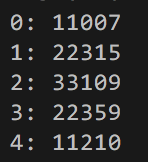 |
| Value distribution for throwing 3-sided-dice two times. |
Ok, that looks exactly like 1, 2, 3, 2, 1
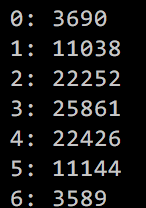 |
| Value distribution for throwing 3-sided-dice three times. |
Now this one is harder, it looks like 1, 3, 6, 7, 6, 3, 1, but I'm not really sure.
What if instead of throwing random simulation, we look exactly at the actual possible values?
 |
| Simulation2 |
Calculating the frequency of each value from that code get us exactly:
[1,2,3,2,1].
Neat, the first one is correct, what about the 2nd one?
Let's just change our function a bit.
 |
| Fuck reusability, reliability, readability, and speed lol. |
Calculating the frequency of each values gave us:
[1, 3, 6, 7, 6, 3, 1].
Whoa, neat!
Now how can we generalize these values? By creating the
Generalized Pascal Triangle
I don't really know how I get it, this is the point where it just struck your head or something.
 |
| Pascal Triangle for 4-sided-dice |
 |
| Pascal Triangle for 6-sided-dice |
How do we generate these triangles?
For 2 sided coin, everyone probably knows that:
pt2[x] = pt2.parent[x - 1] + pt2.parent[x]
or, if you're more mathematic wired, we can represent it like this as well:
pt2[x] = pt2[x - 1, y - 1] + pt2[x, y - 1]
So, how about 4 sided dice?
It's not much different.
pt4[x] = pt4[x - 3, y -1] + pt4[x - 2, y - 1] + pt4[x - 1, y - 1] + pt4[x, y - 1]
Notice the formula?
yeah, it is:
ptN[x] = sum(ptN[x - N + i, y] for i in xrange(1, N - 1))
legends: ptN[x, y] = Pascal Triangle for N sided-dice at (x, y)
can we optimize this calculation? yeah, we can, but it's not necessary, (be warned, I don't actually implemented this, so I can't guarantee the formula, it might have an off-by-one-error)
ptAN[x, y] = ptAN[x - N + i, y] + ptN[x, y]
legends: ptAN[x, y] = Pascal Triangle Accumulative Value.
it's probably also more useful to store its accumulative value instead of its actual value, so my array would look like this:
 |
| Pascal Triangle (Accumulative) for 4 sided dice. |
This way, if I were to figure out the probability of X >= X' when you throw 4 sided dice with value (0, 1, 2, 3) 2 times.
I just need to calculate:
P(X >= X') = ptA4[X', 2] / ptA4[0, 2]
Notice that I said the value of our dice is (0, 1, 2, 3) while the value of dice in the problem is (1, 2, 3, 4), so we should also tweak our implementation a little. The good part is it is trivial, but the bad part it's also where the bugs may arise from.
As for closing remarks:
I personally consider these problems a good one actually, or not, it's just that I like these kind of question because it fit my strong point.
Finally, have this gem from 2011.










